Sommige mensen huiveren bij het woord ‘algebra’, terwijl anderen er spontaan een glimlach van op hun gezicht krijgen. Toch hebben online rekenraadsels iets magisch.
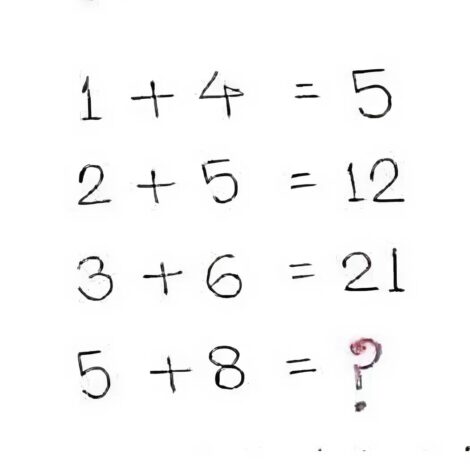
Zodra er zo’n ogenschijnlijk eenvoudige puzzel verschijnt, gaan duizenden nieuwsgierige breinen ermee aan de slag. Het internet loopt er warm voor, discussies barsten los en iedereen wil als eerste met dé oplossing komen. Dat wiskunde op school ooit frustrerend was, doet er opeens niet meer toe.
Deze puzzels hebben weinig gemeen met saaie lesboeken. Ze prikkelen het brein, dagen uit tot anders denken en leveren vaak een euforisch moment op zodra het kwartje valt.
Dat is precies waarom ze zo populair zijn. Een rekenraadsel dat momenteel flink rondgaat op sociale media lijkt simpel: enkele optelsommen waarbij het laatste antwoord ontbreekt. Maar wie even de tijd neemt, merkt dat de uitkomsten niet kloppen volgens het standaard rekenwerk. En daar begint het avontuur.
De sommen zijn als volgt opgesteld:
1 + 4 = 5
2 + 5 = 12
3 + 6 = 21
5 + 8 = ?
Op het eerste gezicht zou je 5 + 8 = 13 verwachten. Maar niets is minder waar. Want waarom is 2 + 5 ineens 12? Of 3 + 6 ineens 21? De uitkomsten lijken uit de lucht gegrepen, maar juist dat maakt het interessant.
Mensen gaan verbanden zoeken, patronen herkennen en zelfs hun kennis van getalsstelsels afstoffen. Het is geen exacte wetenschap meer, maar een speelse zoektocht naar logica.
Eén veelgenoemde oplossing rekent als volgt: neem de som van de getallen en tel daarbij het product van beide getallen op. Dus: 5 + (5 × 8) = 45.
Een uitkomst die verrassend logisch blijkt zodra je dit patroon op de eerdere sommen toepast. Maar daar blijft het niet bij. Er is namelijk ook een aanpak waarbij je telkens de vorige uitkomst meeneemt in de berekening. In dat geval krijg je: 5 + 8 + 21 = 34. Een slimme methode die meer draait om reeksdenken dan om kale getallen.
Andere puzzelaars ontdekken patronen waarbij getallen systematisch verhoogd worden volgens een onzichtbare regel. Dit levert opnieuw 34 op, al moet je goed kijken om de volgorde te doorgronden.
Nog creatievere breinen duiken in alternatieve getallenstelsels. In binaire vorm zou 13 bijvoorbeeld gelijk zijn aan 1101. En in het drie-tallig stelsel verandert het zelfs in 111. Dat vereist wel even schakelen, maar het laat zien hoe breed wiskundig denken kan zijn.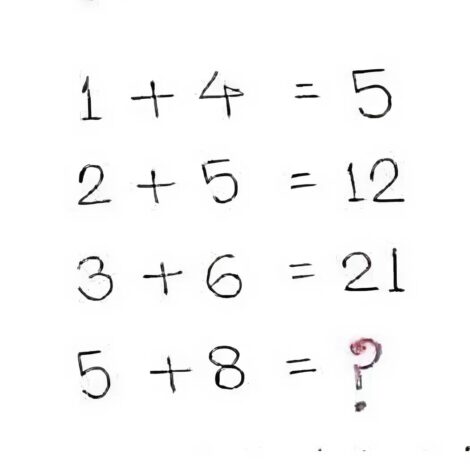
Wat deze puzzel zo bijzonder maakt, is het feit dat er niet één heilig antwoord is. Meerdere uitkomsten kloppen – zolang je je logica maar consistent toepast.
Hierdoor voelt het oplossen van zo’n raadsel eerder als een kunstvorm dan als een exacte rekensom. Het stimuleert creativiteit, daagt je denkpatronen uit en levert vaak verrassend veel voldoening op.
Dus, waar kwam jij op uit? Was het 45, 34 of misschien iets compleet onverwachts? Deel jouw redenering in de reacties op Facebook en ontdek hoe anderen dit raadsel aanpakken.
Misschien inspireer je iemand met jouw kijk op cijfers – of krijg je zelf een nieuw inzicht dat het mysterie nóg interessanter maakt.
